Explain the Main Differences Between Definite and Indefinite Integral Calculus
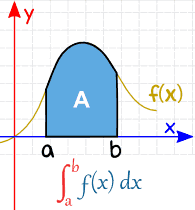
Definite Integral and indefinite integral are two useful categories that are used to solve many real-life problems and the fundamental theorem of integral calculus connects the derivative and the integral. For any function ƒ which is not necessarily non-negative and defined on the interval ab a b ƒ x dx is called the definite integral ƒ on ab.

Calculus Lesson 16 Indefinite And Definite Integrals Don T Memorise Youtube
The definite integral is defined to be exactly the limit and summation that we looked at in the last section to find the net area between a function and the x-axis.

. The indefinite integrals are not bounded from both the endpoints. In this section aspirants will learn about the indefinite and definite Integration list of important formulas how to use integral properties to solve integration problems integration methods and many more. If the specific interval is mentioned then it is known as definite integral otherwise indefinite integral.
Explain the difference between an indefinite integral and a definite integral. 6 rows The main difference between Definite and Indefinite Integral is that a definite integral. 2nd we need to add a c to all of our equations.
The indefinite integral is similar to. An indefinite integral is also defined and continuous over the interval of integration but may have to as a limit of integration OB. Later in this chapter we examine how these concepts are related.
A definite integral results in a set of. Explain the difference between an indefinite integral and a definite integral. An indefinite integral is a family of functions.
An indefinite integral after evaluating it at the limits of integration results in a particular number. The indefinite integral is an easier way to signify getting the antiderivative. But for definite integration both endpoints are specific and definite.
It can be visually represented as an integral symbol a function and then a dx at the end. 1st we will get an equation for our answer rather than a value. An indefinte integral cannot always be integrated analytically and may require numeric integration while it is always possible to integrate a definite integral.
It is depicted by the symbol. Definite integrals aways return a real number after evaluation at its limits of integration OD. If ƒ x F x then ƒ x dx F xC where C is a constant ƒ x dx is called the indefinite integral of ƒ x.
Calculus questions and answers. Unlike the definite integral the indefinite integral is a function. It means the independent variable will not have any given interval.
The reason for this will be apparent eventually. In definite integrals the integration gives a finite number. Also note that the notation for the definite integral is very similar to the notation for an indefinite integral.
As integration and differentiation are just the inverse of each other the integration may provide the original function if derivative is known. The indefinite integral is defined as a function that will. A definite integral has upper and lower limits on the integrals and its called definite because at the end of the problem we have a number - it is a definite answer.
Be sure to include. Definite integrals always return a real number after evaluation at its limits of integration. An indetinte integral cannot always be integrated analytically and may require numeric integration while it is always possible to integrate a definite integral Definite integrals always return a real number atter evaluation at its limits of integration Oc.
Since the indefinite integral doesnt have bounds two things will be different from calculating a definite integral. A definite integral is defined and continuous over the interval of integration and has finite limits of integration. If f is the derivative of F then F is an antiderivative of f.
Be sure to include what form the answers to each integral take function number etc and what the answers mean. In other words indefinite integrals and antiderivatives are essentially reverse derivatives. Integral calculus is the branch of calculus where we deal with the theory properties and applications of Integral.
So lets think about what F of b minus F of a is what this is where both b and a are also in this interval. Now what I want to do in this video is connect the first fundamental theorem of calculus to the second part or the second fundamental theorem of calculus which we tend to use to actually evaluate definite integrals. It is also described as the fundamental theorem of calculus.
A definite integral is a number. Also in this section we are introduced to some new integrals. So the two integrals are independently defined concepts.
An indefinite integral after evaluating it at the limits of integration results in a particular number. It is also called as the antiderivative. The indefinite integral is by definition the primitive of a function or its antiderivative hence it is related by definition to the concept of derivative.
The definite integral is by definition a limit of a certain class of sums the class of the Riemann sums by the way. We also call F the indefinite integral of f. No relation a priori with the derivatives.
An indefinite integral is a function that practices the antiderivative of another function. Keep going and youll find out. A definite integral is defined and continuous over the interval of integration and has finito limits of integration An indefinite.
However close attention should always be paid to notation so we know whether were working with a definite integral or an indefinite integral. A definite integral results in a set of. Integration is the reverse of differentiation.
An indefinite integral after evaluating it at the limits of integration fosults in a particular number. Indefinite integrals associate an arbitrary variable hence the family of functions and definite integrals do not have an arbitrary constant but an upper limit and a lower limit of integration. Subsection 152 Definite Integral versus Indefinite Integral Due to the close relationship between an integral and an antiderivative the integral sign is also used to mean antiderivative.
With an indefinite integral there are no upper and lower limits on the integral here and what well get is an answer that still has xs in it and will also have a K plus K in it. An indefinite integral cannot always be integrated analytically and may require numerio integration while it is always possible to integrate a definite integral. Why differentiate in reverse.
Indefinite Integral vs Definite Integral.

Indefinite Integrals At A Glance

Calculus Antiderivatives And The Indefinite Integral Mathematics Stack Exchange

Solved A Explain The Difference Between An Indefinite Chegg Com

Definite Integrals Reverse Power Rule Video Khan Academy

Lesson Explainer Properties Of Definite Integrals Nagwa

Calculus Change Of Variables For Definite Integrals Mathematics Stack Exchange

Solved Explain The Difference Between An Indefinite Integral Chegg Com

Definite Integral Calculus Examples Integration Basic Introduction Practice Problems Youtube

Definite Integral Of Rational Function Video Khan Academy

Fundamental Thereom Of Calculus Explained Part 1 2 Examples Definite Integral Youtube

What S The Difference Between A Definite Integral And An Indefinite Integral Calculus Youtube

Ap Calculus Exam Review Integrals Magoosh Blog High School

What Is The Difference Between A Definite And Indefinite Integral Socratic
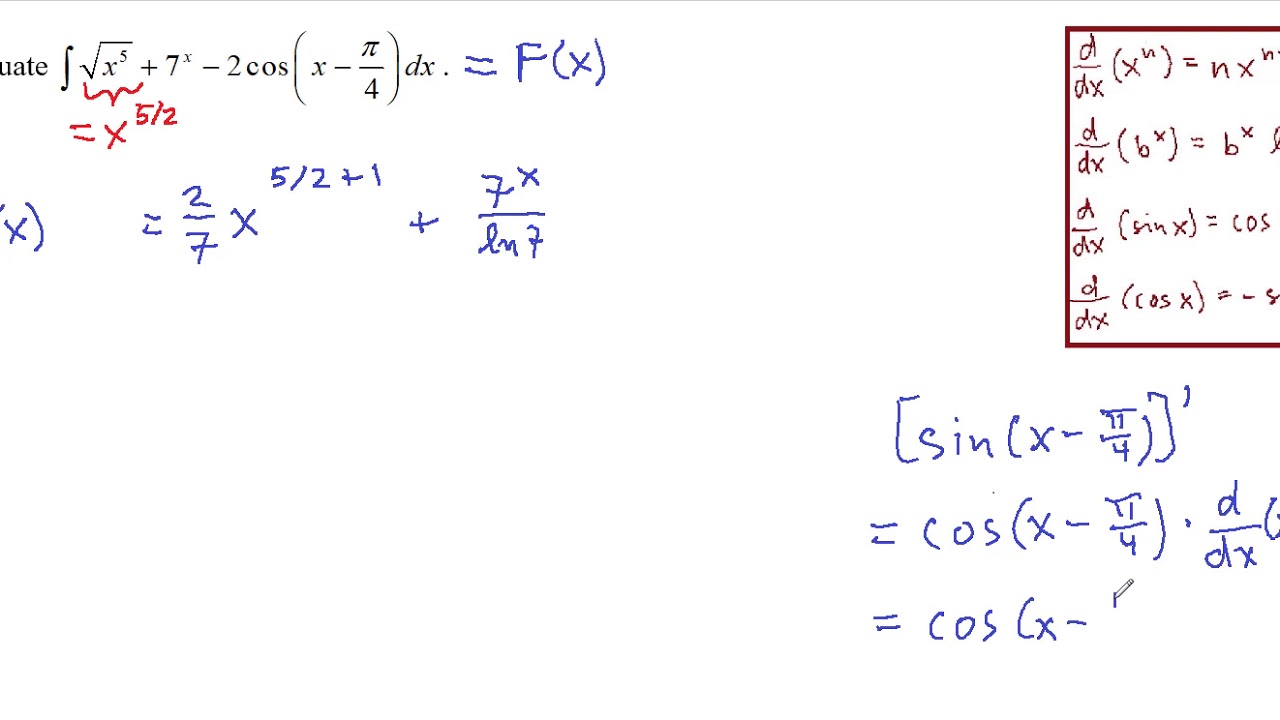


Comments
Post a Comment